ANALISIS DE FALLA
Los siguientes son los pasos recomendados en un análisis de falla
1.- Datos del medioambiente
2.- Selección apropiada de las muestras
3.- Examen visual preliminar de la pieza fallada
4.- Ensayos no destructivos
5.- Análisis químico
6.- Características mecánicas de las piezas falladas
7.- Análisis microscópico óptica y electrónica
8.- Determinación de los micro mecanismos de fractura
9.- Ensayos bajo condiciones de servicio (lo más cercano a la realidad) puede ser un
ensayo virtual por computador
Otros autores recomiendan lo siguiente:


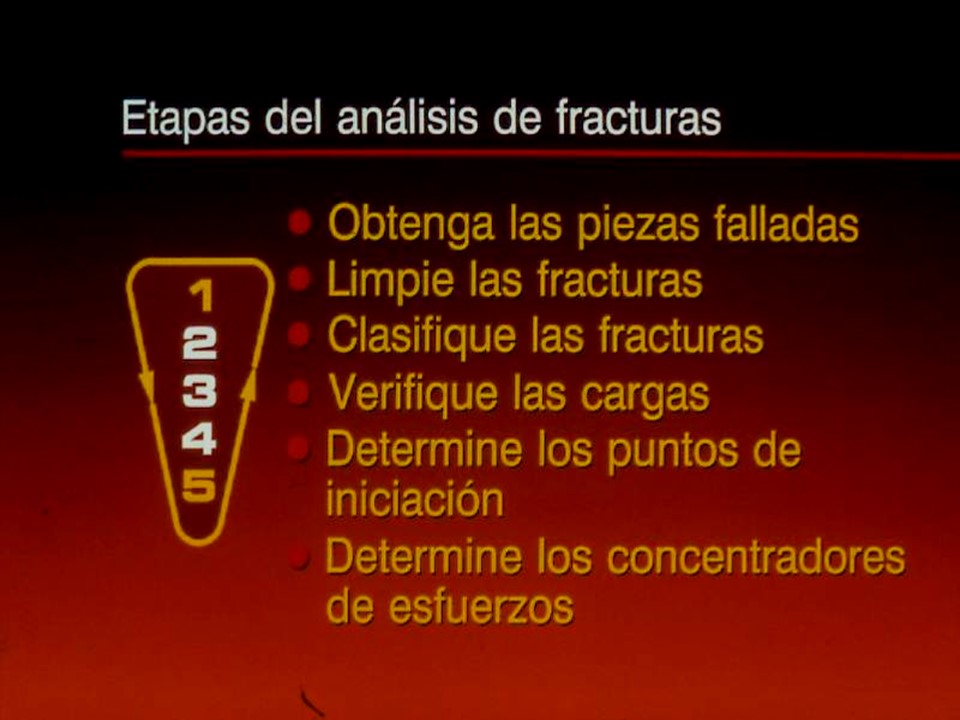

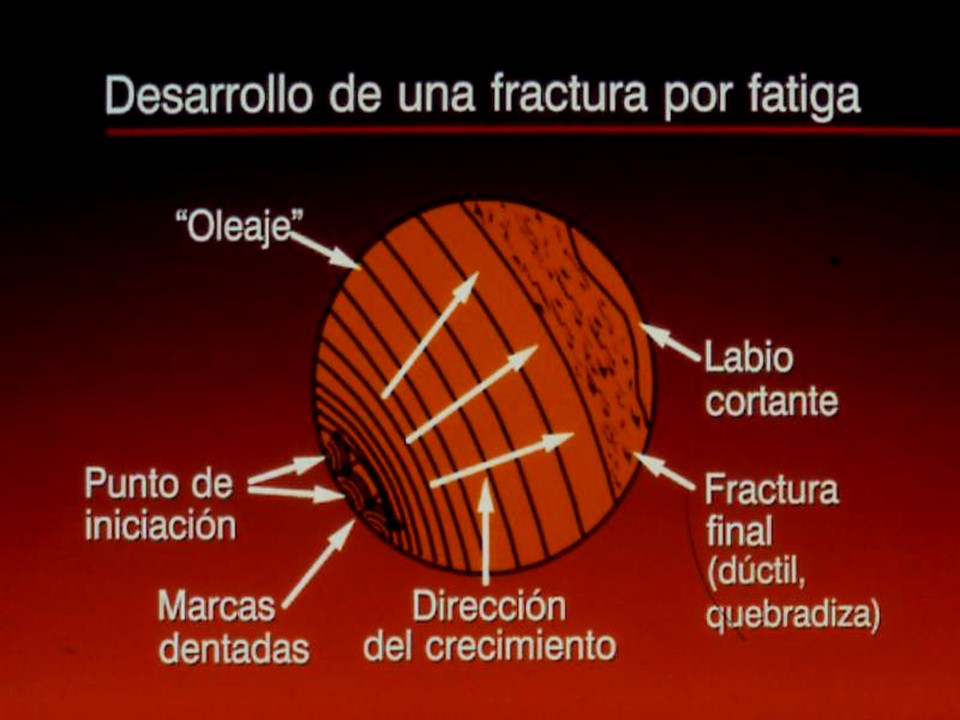
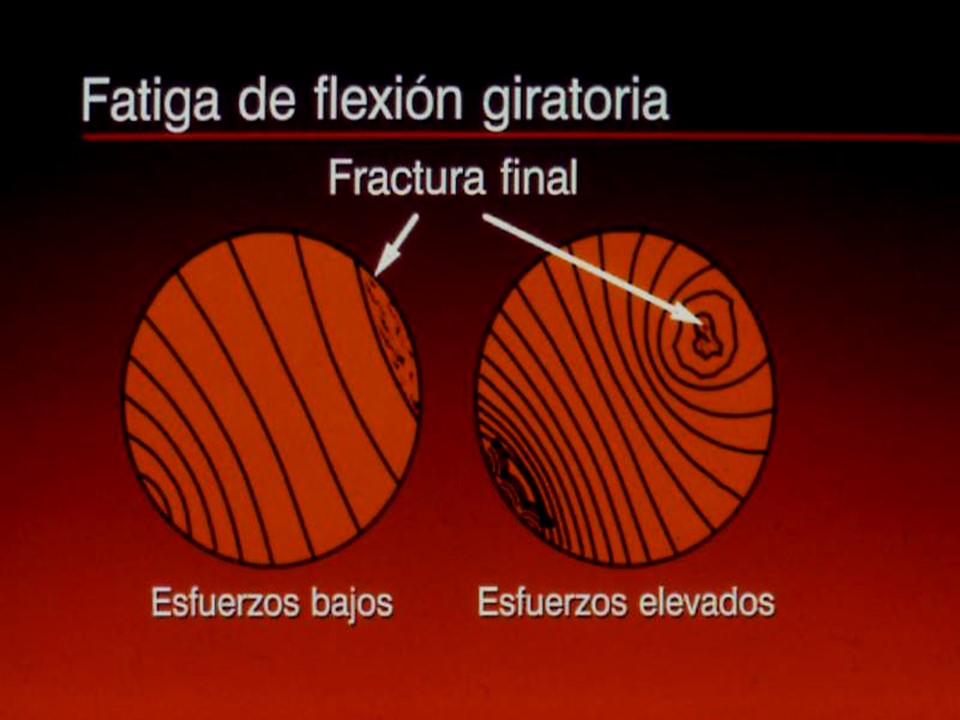

SERVICIOS
Ingeniería Multidisciplinaría.
Modelación Computacional.
Inspección Técnica de Obra.
Distribución deSoftware.
Fabricación de Estructuras.
CONTACTOS
ANTOFAGASTA, CHILE
(+56) 9 9919 0294
ventas@cad-cae.com












